发表于 更新于

基础知识

https://www.cnblogs.com/ink599/p/18666435
【【ECC加密算法】| ECC加密原理详解| 椭圆曲线加密| 密码学| 信息安全】https://www.bilibili.com/video/BV1v44y1b7Fd?vd_source=ff68aa66b51da907e9343d02f7f03e91
大概了解了一下基础知识，第一个就是概念题

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from Crypto.Util.number import getPrime
from libnum import s2n
from secret import flag

p = getPrime(256)
a = getPrime(256)
b = getPrime(256)
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = getPrime(256)
K = k * G
r = getPrime(256)
c1 = m + r * K
c2 = r * G
cipher_left = s2n(flag[:len(flag)//2]) * m[0]
cipher_right = s2n(flag[len(flag)//2:]) * m[1]

print(f"p = {p}")
print(f"a = {a}")
print(f"b = {b}")
print(f"k = {k}")
print(f"E = {E}")
print(f"c1 = {c1}")
print(f"c2 = {c2}")
print(f"cipher_left = {cipher_left}")
print(f"cipher_right = {cipher_right}")

'''
p = 74997021559434065975272431626618720725838473091721936616560359000648651891507
a = 61739043730332859978236469007948666997510544212362386629062032094925353519657
b = 87821782818477817609882526316479721490919815013668096771992360002467657827319
k = 93653874272176107584459982058527081604083871182797816204772644509623271061231
E = Elliptic Curve defined by y^2 = x^3 + 61739043730332859978236469007948666997510544212362386629062032094925353519657*x + 12824761259043751634610094689861000765081341921946160155432001001819005935812 over Finite Field of size 74997021559434065975272431626618720725838473091721936616560359000648651891507
c1 = (14455613666211899576018835165132438102011988264607146511938249744871964946084 : 25506582570581289714612640493258299813803157561796247330693768146763035791942 : 1)
c2 = (37554871162619456709183509122673929636457622251880199235054734523782483869931 : 71392055540616736539267960989304287083629288530398474590782366384873814477806 : 1)
cipher_left = 68208062402162616009217039034331142786282678107650228761709584478779998734710
cipher_right = 27453988545002384546706933590432585006240439443312571008791835203660152890619
'''

exp

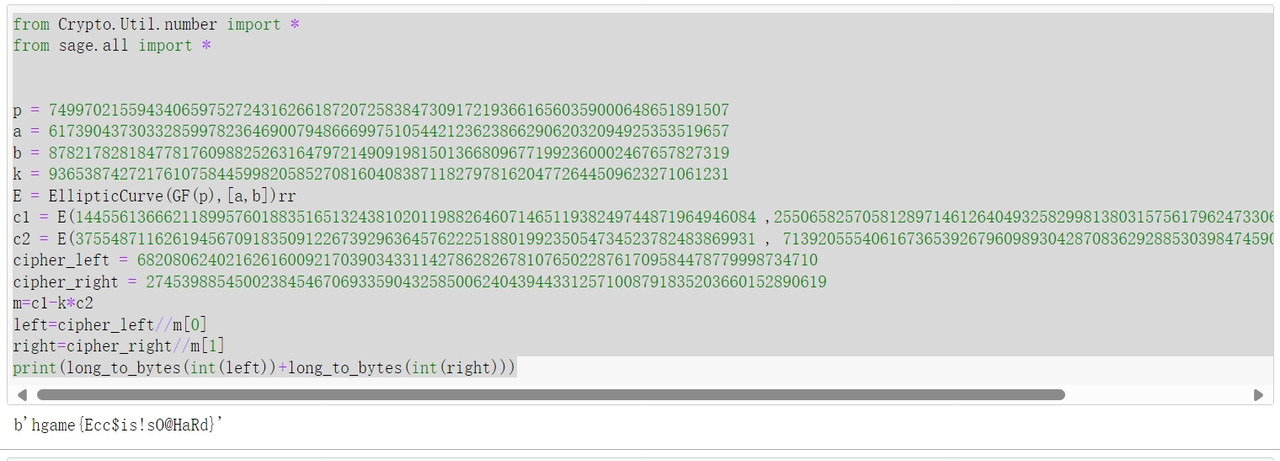
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from Crypto.Util.number import *
from sage.all import *


p = 74997021559434065975272431626618720725838473091721936616560359000648651891507
a = 61739043730332859978236469007948666997510544212362386629062032094925353519657
b = 87821782818477817609882526316479721490919815013668096771992360002467657827319
k = 93653874272176107584459982058527081604083871182797816204772644509623271061231
E = EllipticCurve(GF(p),[a,b])
c1 = E(14455613666211899576018835165132438102011988264607146511938249744871964946084 ,25506582570581289714612640493258299813803157561796247330693768146763035791942,1)
c2 = E(37554871162619456709183509122673929636457622251880199235054734523782483869931 , 71392055540616736539267960989304287083629288530398474590782366384873814477806,1)
cipher_left = 68208062402162616009217039034331142786282678107650228761709584478779998734710
cipher_right = 27453988545002384546706933590432585006240439443312571008791835203660152890619
m=c1-k*c2
left=cipher_left//m[0]
right=cipher_right//m[1]
print(long_to_bytes(int(left))+long_to_bytes(int(right)))