Crypto

1、Hello crypto

解题思路：

非常简单的签到题。

import libnum
m = ...

flag = libnum.n2s(m)
print(flag)

2、EzAES

解题思路：

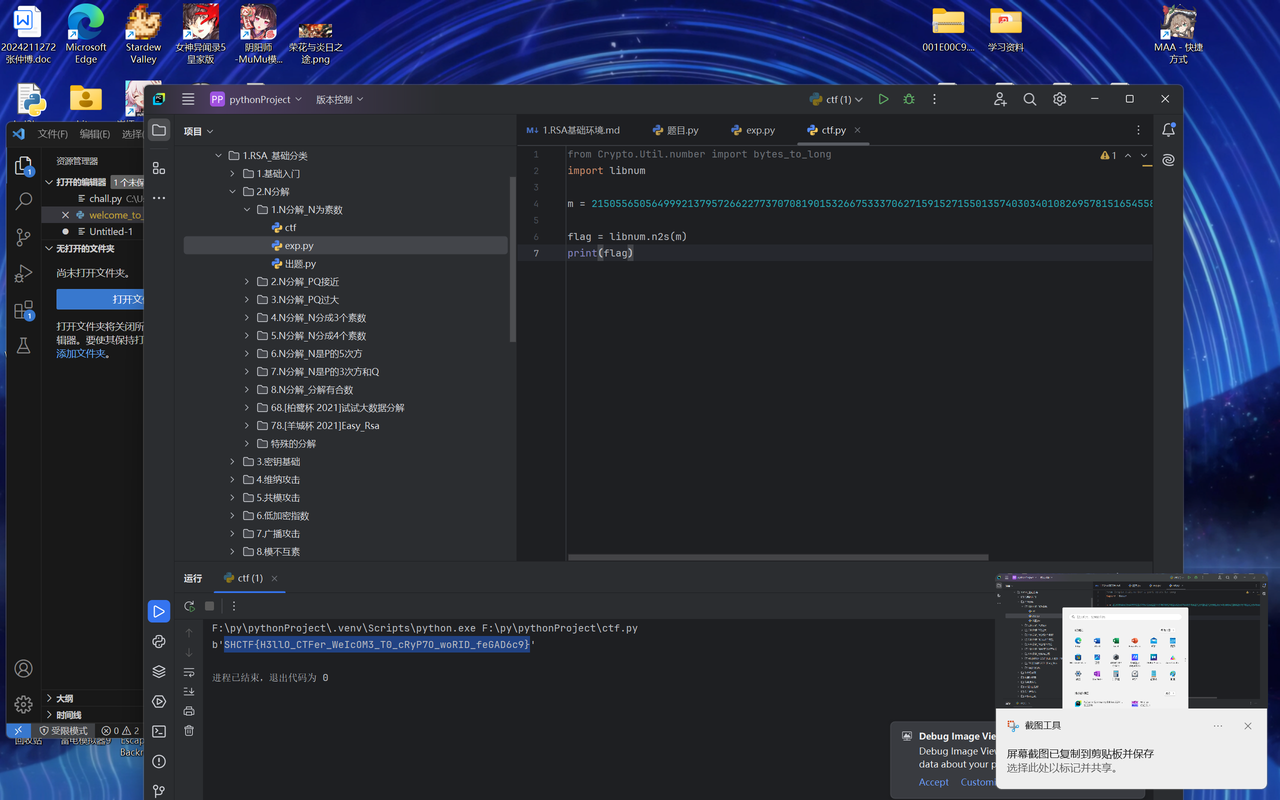
依旧是附件，据hint用utf-8编码打开（实际上直接用vscode打开就可）

题目直接给出了c iv key的具体值（这里的iv和key是随机生成的密钥）那么直接求解

from Crypto.Cipher import AES


key = b'\xf8\x0c"\xa0m\x94\xc0\xee\xd6\xd3zA\xf1+\xac\xc5'
iv = b'\xb8\xce418z\x8b\xb70\x80Q\xc3\xd6\xf6$\xdd'
c=b'\xa5\x94\xc6\x1a\xc8\xac\xef\x96\xdc\x11~F\xc1r\x14\xd1\x18\xf6\xe87\x80|\xc6<\xe3&\xa2T\x8a\xf4\xf8\xac\xbb\x82\xe7bv\x005\x90R\xd8\xea\x9f\x8e\xd3+\x8a'

my_aes = AES.new(key, AES.MODE_CBC, iv)

# 解密数据
decrypted_flag = my_aes.decrypt(c).rstrip(b' ')  # 移除填充的空格
print(decrypted_flag)

弯路：

显然刚用vscode打开时有点懵，不同于其他rsa加密，遂逐渐唤醒之前学过aes的记忆，尝试直接在线解密（因为不会写脚本），最后gpt大法！

3、d_known

解题思路:

读题，依旧是密文m 以及素数qp，但这里qp为相邻的素数，接着告知了d、c，直接开解

import math
import libnum
import gmpy2
import sympy

# 已知数据
d = ...
e = 0x10001
c = ...

ed1=e*d-1     #ed-1=k(p-1)(q-1)
for k in range(65537,1,-1):   #从65537开始递减
    if ed1%k==0:
        phi=ed1//k
        p1,s1=gmpy2.iroot(phi,2)#这里做的开放处理是因为近似qp相等
        p=gmpy2.next_prime(p1)
        if phi%(p-1)==0:
            q=sympy.prevprime(p)
            break
n=p*q
m=pow(c,d,n)
print(libnum.n2s(int(m)))

弯路：

整体过程异常曲折，首先重温rsa的基本加密步骤。附上一篇感觉写的很清楚的文章https://www.ruanyifeng.com/blog/2013/07/rsa_algorithm_part_two.html#:~:text=第一步，随机
1.怎么将qp表示出来
2.开方处理后怎么确保p-1 or q-1的范围是否跳脱了原本q和p的范围，即能不能确认这个next prime就是p or q，故尝试补上一些数，发现没用，最后结果并不用考虑…
3.k这个取值范围的考虑，一开始ai做出来的脚本大多都是递增，导致跑不出来，然后递减再做就ok了。

4、factor

解题思路：

这次告诉了N c e的值，依旧是rsa加密，那么从头开始看，定义proc函数，接着取10个任意64位质数作为prime_list，十个质数乘起来作为N，而从这十个选取7个相乘作为n，然后一切照旧。
步骤：1、分解N (yafu真好用)

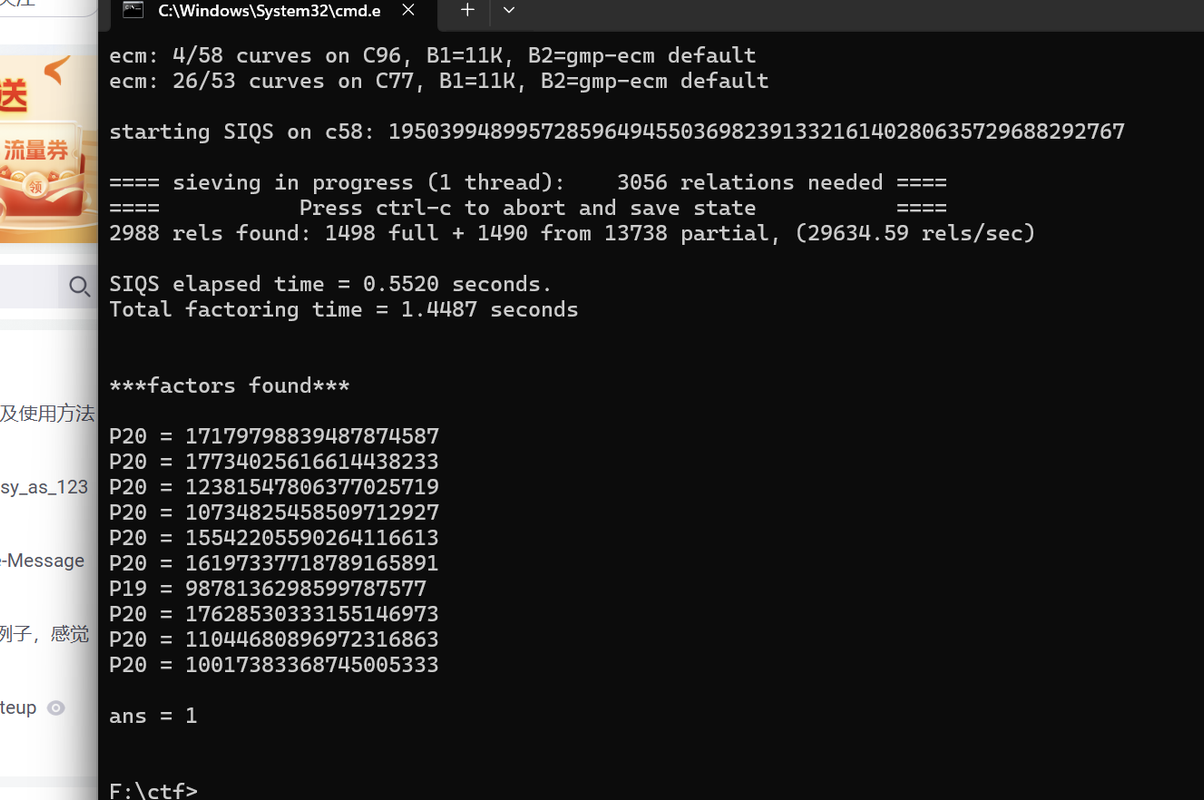
2、列出n可能的情况进行求解

from itertools import combinations
from functools import reduce
from Crypto.Util.number import long_to_bytes, inverse

# 已知的 10 个素数
prime_list = [
    17179798839487874587,
    17734025616614438233,
    12381547806377025719,
    10734825458509712927,
    15542205590264116613,
    16197337718789165891,
    9878136298599787577,
    17628530333155146973,
    11044680896972316863,
    10017383368745005333
]

# 已知的公钥指数 e 和密文 c
e = 65537
c = 26766985375623703113904250876884598223156426789118183045142542215836711584140516370218654279179189004314203387292364759414400477630158

# 找到所有 7 个素数的组合
possible_combinations = list(combinations(prime_list, 7))

# 遍历每个组合，计算可能的 n 并尝试解密
for comb in possible_combinations:
    # 计算模数 n 和欧拉函数 phi_n
    n = reduce(lambda x, y: x * y, comb)
    phi_n = reduce(lambda x, y: x * (y - 1), comb, 1)

    try:
        # 计算私钥 d
        d = inverse(e, phi_n)

        # 尝试解密密文
        m = pow(c, d, n)

        # 将解密后的消息转换为字节形式
        plaintext = long_to_bytes(m)

        # 打印解密结果（可能的 flag）
        print(f"Possible flag with n = {n}: {plaintext.decode()}")

    except ValueError:
        # 如果计算 d 或解密失败，则跳过此组合
        continue

补充reduce函数：

1、reduce(lambda x, y: x * y, comb) 使用 Python 的 reduce 函数，对组合 comb 中的所有素数执行连续的乘法运算。
2、reduce(lambda x, y: x * (y - 1), comb, 1) 使用 reduce 函数，对组合 comb 中的每个素数 p进行p-1，即计算欧拉函数。

弯路：

1、寻找质数分解工具。在网上搜寻了好久，发现没有类似的中文在线网站可以分解这种质数，我甚至猜测是不是可以不用分解，发现不现实，但最后找到了yafu。
2、yafu的正确使用，这里贴上一些用法吧

1、如果数比较小，进入该文件的目录后可以直接使用：

yafu-x64 factor(23333333333333)
如果是powershell，则使用：

.\yafu-x64 factor(23333333333333)
2、如果数比较大，那就需要将数保存成一个txt，然后使用，powershell则是在前面加.\：

yafu-x64 “factor(@)” -batchfile n.txt

5、baby_mod

解题思路：

给出已知数leak r t 以及p q tmp的位数
那么已知tmp的位数很小，所以枚举非常好算。
tmp属于(2^14 2^15)这个范围;
又已知leak = pr - qt -tmp(leak为负数),
代换一下-leak-tmp = c1 =qt-pr(直接看做c1为常数);
接下来就是怎么解方程:
我们不妨设t1使得 t * t1 % r = 1,
上式两边同乘t1 再同取余r ,
便得到了q的表达式.
给出具体代码：

from Crypto.Util.number import long_to_bytes, inverse
from sympy import isprime, primerange
import libnum

# 已知的数据
c = ...
leak = -192....
r = ...
t = ...
e = 65537

tmp_list = list(primerange(2**14, 2**15))
for tmp_guess in tmp_list:
    c1 = -tmp_guess - leak
    if c1>0:
        t1 = libnum.invmod(t, r)  # 或者用 gmpy2.invert(r, t)
        q = (c1 * t1) % r  # 直接取模运算
        p = (t * q - c1) // r  # 计算 q
        if isprime(p) and isprime(q):
            n = p * q  # 得到模数 n
            phi = (p - 1) * (q - 1)  # 欧拉函数
            d = libnum.invmod(e, phi)  # 计算私钥 d
            m = pow(c, d, n)  # 解密
            print(libnum.n2s(m))  # 输出明文

弯路:

1、经过搜索其实是找到了相关的例题，贴下链接
https://blog.csdn.net/figfig55/article/details/128496397#:~:text=大概逻辑就是
但很明显，不能直接用，该题存在temp这一值，所以从头分析，就有了开头的代换，将未知转已知。
2、接着是两个if条件判断，但一开始我并未意识到这个leak这么小，所以我在设置c1>0后跑不出来flag，而程序检查也没有错误，最后发现要再颠倒一次，于是开头的c1略显诡异。

git

发表于 2025-08-13 更新于 2025-08-14

Git 终端使用

前言

此次记录目的为记录第一次通过终端完成 git 仓库的拉取、推送等操作，以及一些可能常出现的错误

git config 配置

安装好 git 后可通过 git bash 打开，也可直接通过 shell 进行操作

用户名和邮箱配置

1 2	git config --global user.name "name" git config --global user.email "example@email.com"

代理的配置、取消与查看

# 配置
 git config --global http.proxy http://127.0.0.1:33210
 git config --global https.proxy http://127.0.0.1:33210
# 取消
 git config --global --unset http.proxy
 git config --global --unset https.proxy
# 查看
 git config --global --get http.proxy
 git config --global --get https.proxy

搭建本地仓库，并链接自己的远程仓库

在本地新建一个文件夹，通过终端进入
1
2
# 创建仓库
git init
添加文件或文件夹到暂存区
1
2
3
git add .

git add [文件名]

提交到本地仓库

1
2
3

git commit -m "first"

git commit -am "second"

github 创建远程仓库
建立完成后在 code 下找到该仓库链接并复制，而后在终端操作
1
git remote add origin "地址"
ssh 公钥设置与检查
1
ssh-keygen -t rsa -C "邮箱名"
然后进入保存 ssh 的文件，打开 id_rsa.pub，复制而后在 github 个人设置中添加
1
2
# 检查
ssh -T git@github.com
出现 successfully就成功
推送
1
git push -u origin master

拉取

git pull origin master

git fetch origin master

git merge origin master

问题

拉取别人仓库文件到本地时，会出现 origin 已配置，原因是一个远程仓库已经被命名为 origin ，不能再次指向另一个仓库
1
2
3
4
# 删除已有的仓库
git remote rm origin
#添加
git remote add origin "仓库地址"
1
2
# 换名字
git remote add origin2 "仓库地址"
git push 推送问题
- ! [rejected] master -> master (non-fast-forward)
  远程库已有代码，出于安全不允许直接推送，先将远程库的文件 pull 过来或者 fetch（前者会直接让本地库被覆盖）
1
2
3
4
5
git pull origin master

# 使用 fetch 和 merge
git fetch origin master
git merge origin master
此操作可能出现
refusing to merge unrelated histories
1
2
# 添加后缀
git pull origin master --allow-unrelated-histories
而后提交当前变化，即再 add 和 commit 一次
最后 merge 后即可提交

也可以 git push -f 强推，不建议
- ! [rejected] master -> master (fetch first)
  远程库和本地库版本不一致，解决方案与上述类似，拉取远程库后合并再推送
- 部分未推送
  常见原因有：本地仓库为空（未 add ）；add 后未 commit ； git init 错误
return error 403
此问题出现于 git push 不加参数默认推送到主分支时，原因是需要令牌（鉴权失败也同理）

记得复制令牌后保存到别处，否则会刷新掉

whi

ecc1

shctf

Crypto

1、Hello crypto

解题思路：

2、EzAES

解题思路：

弯路：

3、d_known

解题思路:

弯路：

4、factor

解题思路：

补充reduce函数：

弯路：

5、baby_mod

解题思路：

弯路:

git

前言

git config 配置

搭建本地仓库，并链接自己的远程仓库

问题